这篇文章写自英文，阅读原文章.
由于本文暂未被翻译成中文，请使用下面工具选项进行翻译

本报告仅供参考和个人研究。 关于疫情的最新动态请访问：
For detailed data: 新型冠状病毒肺炎追踪
最新新闻: COVID-19 alert

INTRODUCTION

Background

Currently, our daily life is profoundly impacted by the outbreak of the Coronavirus disease 2019 (COVID-19), and the number of confirmed cases has quickly increased in the past few weeks. Starting mid-March, States, Companies, Businesses, Schools are beginning to take action to respond to the outbreak. States are promoting residents to stay at home, Companies are promoting remote working, Businesses are starting to suspend their operation, and schools are beginning to transform to E-Learning. All of these are acting as a part of social distancing. Research shows Social distancing can highly reduce the infection of infectious disease. A model shows that if 25% of the residents reduce daily social interactions to 50%, the number of primary infections can be reduced by 81% (Maharaj).

Orienting Material

a. Using Quadratic Least Squares polynomial to find out the formula of the new cases of COVID-19 over a period of time.
b. Using Richardson’s Extrapolation to the 3-point midpoint formula to calculate the new cases increased rate of COVID-19.
c. Generate a report for the time period every 7 days starting January 21th.

Thesis

Even though people think the Coronavirus is less serious and quarantine at home has no effect. The purpose of the report is to raise more people’s attention to new Coronaviruses and encourage people to isolate at home because Compared with before, people began to pay attention to the severity of the Coronavirus. And many people began to isolate themselves, and the rate of new patients dropped significantly.

ANALYSIS

Data Collection

a. Our data are collect form 2019 Novel Coronavirus COVID-19 (2019-nCoV) Data Repository by Johns Hopkins CSSE which their data was collected from WHO, CDC, ECDC, NHC, DXY, 1point3acres, Worldometers.info, BNO, the COVID Tracking Project, state and national government health departments, and local media reports (Dong). They also promise that the data will be updated frequently. The data will be provided containing the Federal Information Processing Standards code (Dong); County name; Province, state or dependency name; Update time; Geocode; Confirmed case number; Deaths case number; Recovered number; Active number. In summary, the source is creditable and usable.
b. Data Table

Week Number Start Date End Date New Case Total Case
Week1 01-21-20 01-27-20 5 5
Week2 01-28-20 02-03-20 6 11
Week3 02-04-20 02-10-20 1 12
Week4 02-11-20 02-17-20 0 12
Week5 02-18-20 02-24-20 2 14
Week6 02-25-20 03-02-20 43 57
Week7 03-03-20 03-09-20 588 645
Week8 03-10-20 03-16-20 3728 4373
Week9 03-17-20 03-23-20 38378 42751
Week10 03-24-20 03-30-20 117935 160686
Week11 03-31-20 04-06-20 202357 362952
Week12 04-07-20 04-13-20 215226 578178
Week13 04-14-20 04-20-20 197672 775850
Week14 04-21-20 04-27-20 206800 982650

^Download daily/monthly table
c. Data Graph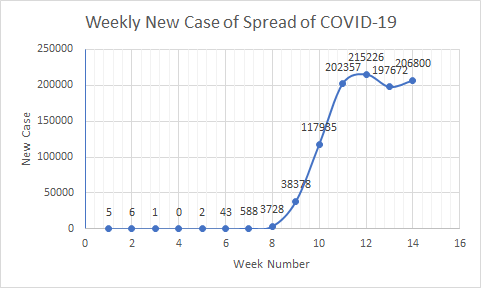
weekly table

Quadratic Least Squares polynomial

Quadratic_least_squares_polynomial.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
%% Quadratic least squares polynomial
close all
clear
clc

x = [50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 ]';
y = [291 269 393 565 662 676 872 1291 2410 3948 5417 6271 8631 10410 9939 12226 17050 19046 20093 19118 20463 25396 26756 28879 32525 33725 25717 29359 30512 32282 34243 33578 31869 28057 24685 25987 29465 32076 30915 28084 26013 25132 25178 29246 32331 36137 34956 26929 22023]';

A = [x.^2 x ones(size(x))];
d = ((A'*A)^(-1)) * A' * y;
a = d(1); b = d(2); c = d(3);
fprintf('Model: f(x) = (%.5f)*x^2 + (%.5f)*x + (%.5f)\n', a, b, c)

hold on
plot(x,y,'r*')
pp=@(t) a.*t.^2+b.*t+c;
plot(x,pp(x))
xlabel('x')
ylabel('y')
title('Days Vs. New Confirm Cases')
legend('Actual data','Quadratic least','location','best')
box on; grid on;

^Download Mathlab Code for Quadratic least squares polynomial
^Download Mathlab Code for Cubic least squares polynomial

Model: $$f(x)=(-25.91048)(x)^2+(4572.54925)x-171258.00999$$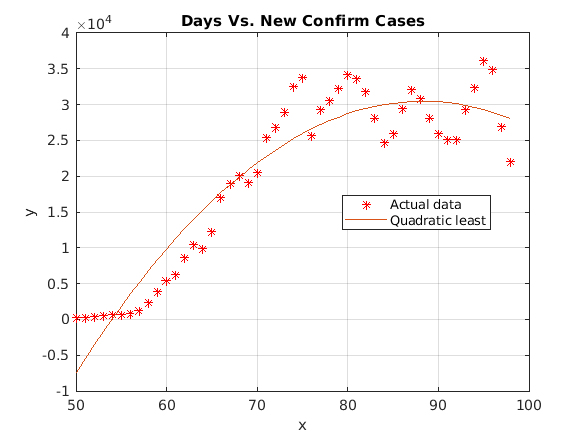
model
Although the data we have is somehow noisy, we can still generate a reasonable model formula by the quadratic least-squares polynomial. We can use the polynomial generated and apply it to Richardson’s Extrapolation to the 3-point midpoint.

Richardson’s Extrapolation to the 3-point midpoint

Once we get a formula by using Quadratic Least Squares polynomial, we can use Richardson’s Extrapolation to the 3-point midpoint to get its first derivative. In numerical analysis, the Richardson extrapolation method can improve the series sequence convergence efficiency. And Richardson’s extrapolation method can generate high-precision results when using low-order formulas (Burden, 185).
The formula we have is $f(x)=(-25.91048)(x)^2+(4572.54925)x-171258.00999$

Richardson_3_point_midpoint.java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.Scanner;

class threePoint {
	static double f(double x) {
    	return (-25.91048)*Math.pow(x,2)+(4572.54925)*x-171258.00999;
	}

	public static void main(String[] args){
    	double h;
    	double first;
    	double inputDay;
    	Scanner scnr = new Scanner(System.in);
    	System.out.println("Please input your h:");
    	h = scnr.nextDouble();
    	System.out.println("Please input your Day:");
    	inputDay = scnr.nextDouble();
    	for(int i = 0; i < 3; i++){
        	double a = 0.5 / h;
        	first = a * (f((inputDay + h)) - f((inputDay - h)));
        	System.out.println("result: " + first);
        	h = h / 2;
    	}
   }
}

^Download python Code for Richardson 3 point midpoint formular
Input day = 60, with h = 4:

result: 1463.2916425999992
result: 1463.2916499999992
result: 1463.2916500000138

$N_1 (4)=1463.2916425999992$
$N_1 (2)=1463.2916499999992$
$N_1 (1)=1463.2916500000138$
$N_2 (2)=N_1 (1)+\frac{1}{3} [N_1 (1)-N_1 (2)]=1463.29165+\frac{1}{3} [1463.29165-1463.29165]=1463.29165$
$N_2 (4)=N_1 (2)+\frac{1}{3} [N_1 (2)-N_1 (4)]=1463.29165+\frac{1}{3} [1463.29165-1463.29164]=1463.29165$
$N_3 (4)=N_2 (2)+\frac{1}{5} [N_2 (2)-N_2 (4)]=1463.29165+\frac{1}{5} [1463.29165-1463.29165]=1463.29165$

Input day = 70, with h = 4:
$N_1 (4)=945.0820499999973$
$N_1 (2)=945.0820499999973$
$N_1 (1)=945.0820499999973$
$N_2 (2)=N_1 (1)+\frac{1}{3} [N_1 (1)-N_1 (2)]=945.08205+\frac{1}{3} [945.08205-945.08205]=945.08205$
$N_2 (4)=N_1 (2)+\frac{1}{3} [N_1 (2)-N_1 (4)]=945.08205+\frac{1}{3} [945.08205-945.08205]=945.08205$
$N_3 (4)=N_2 (2)+\frac{1}{5} [N_2 (2)-N_2 (4)]=945.08205+\frac{1}{5} [945.08205-945.08205]=945.08205$

Input day = 80, with h = 4:
$N_1 (4)=426.8724499999953$
$N_1 (2)=426.87245000000985$
$N_1 (1)=426.87244999998074$
$N_2 (2)=N_1 (1)+\frac{1}{3} [N_1 (1)-N_1 (2)]=426.87245+\frac{1}{3} [426.87245-426.87245]=426.87245$
$N_2 (4)=N_1 (2)+\frac{1}{3} [N_1 (2)-N_1 (4)]=426.87245+\frac{1}{3} [426.87245-426.87245]=426.87245$
$N_3 (4)=N_2 (2)+\frac{1}{5} [N_2 (2)-N_2 (4)]=426.87245+\frac{1}{5} [426.87245-426.87245]=426.87245$

Input day = 90, with h = 4:
$N_1 (4)=-91.33715000000302$
$N_1 (2)=-91.33715000000666$
$N_1 (1)=-91.33715000000666$
$N_2 (2)=N_1 (1)+\frac{1}{3} [N_1 (1)-N_1 (2)]=-91.33715+\frac{1}{3} [-91.33715+91.33715]=-91.33715$
$N_2 (4)=N_1 (2)+\frac{1}{3} [N_1 (2)-N_1 (4)]=-91.33715+\frac{1}{3} [-91.33715+91.33715]=-91.33715$
$N_3 (4)=N_2 (2)+\frac{1}{5} [N_2 (2)-N_2 (4)]=-91.33715+\frac{1}{5} [-91.33715+91.33715]=-91.33715$

CONCLUSION

Summary

Two methods are applied in this project; Quadratic Least Squares polynomial and Richardson’s Extrapolation to the 3-point midpoint. Quadratic Least Squares polynomial is used to discover the formula and the use of Richardson’s Extrapolation to the 3-point midpoint formula is to discover the case increase rate. A graph is generated when Quadratic Least Squares polynomials are calculated in Matlab, which clearly shows the polynomial of the outbreak of COVID-19 over time.

Accuracy

By analyzing the data, we can easily find out that the data is extremely noisy which limits the usage of methods in Numerical Analysis. However, polynomial least squares can solve this problem; it can generate a low-degree polynomial, which can be used to estimate an underlying polynomial (Kalman).
We use Richardson’s extrapolation method for our data analysis, we can see that the results are increasingly converging to the real solution.

Conclusion

From our analysis result above, the Quadratic Least Squares polynomial can give us the best fit line even though we have noisy data. Since many organizations and schools encourage people to isolate themselves, and also the result of the 60th day, 70th day, 80th day, and 90th day gives us the derivative of formula which is the rate of increase, and all these data shows us the new cases keep decreasing. We can easily conclude that with the effort of the social distance, including the hard work of the government official, medical worker, and all the residents in the US, the infection rate will drop into a stable stage and will gradually disappear.

Reference

  1. Burden, Richard L., and J. Douglas. Faires. Numerical Analysis. Brooks/Cole, Cengage Learning, 2011.
  2. Dong, Ensheng, et al. “An Interactive Web-Based Dashboard to Track COVID-19 in Real Time.” The Lancet Infectious Diseases, 19 Feb. 2020, www.thelancet.com/journals/laninf/article/PIIS1473-3099(20)30120-1.
  3. Kalman, R. E. “A New Approach to Linear Filtering and Prediction Problems.” Journal of Basic Engineering, American Society of Mechanical Engineers Digital Collection, 1 Mar. 1960, https://asmedigitalcollection.asme.org/fluidsengineering/article-abstract/82/1/35/397706/A-New-Approach-to-Linear-Filtering-and-Prediction.
  4. Maharaj, Savi, and Adam Kleczkowski . “Controlling Epidemic Spread by Social Distancing: Do It Well or Not at All.” BMC Public Health, 20 Aug. 2012, https://bmcpublichealth.biomedcentral.com/articles/10.1186/1471-2458-12-679.