新冠肺炎和贝叶斯

2020年4月1日更新，根据数据，并没有80%的人生病了第一时间去检测，数据远远超过估算的17813人。详细数据可参考新冠肺炎疫情追蹤 - Bing

英国学者托马斯·贝叶斯(Thomas Bayes)提出了一个定理，这个定理的公式如下
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$
其中A,B是两个随机事件，且B事件的发生概率不为零。

P(A)是A事件会发生的概率，P(B)是B事件会发生的概率，P(A|B)是B发生后A会发生的概率，反之亦然。

打个比方:

P(小明迟到) = 0.3 的意思是小明会迟到的概率为30%

P(老板考察出勤) = 0.2 的意思是老板会考察出勤的概率是20%

P(小明迟到 | 老板考察出勤) = 0.25 的意思是老板考察出勤的时候碰巧小明迟到了的概率是25%

通过上面这三个已知条件，我就能通过贝叶斯公式推测出P( 老板考察出勤 | 小明迟到)，即小明今天迟到了，老板刚好要靠勤的概率。
$$P(老板考察出勤|小明迟到) = \frac {0.25×0.3}{0.2}=0.375$$
我想，我可以用这个公式来推导一下新冠肺炎的真实感染人数。下面的计算过程可能会很枯燥，但是结果很有意思。

我们知道美国的人口大概是327,200,000 (三亿两千七百二十万)。截至三月十九，美国一共测试了103,945(十万三千九百四十五)人，其中检查出14,250(一万四千二百五十人)。我们已知的信息有

1
2
3

N = 327200000 # population in the United States
TESTED = 103945 # total test
POSITIVE = 14250 # positive case

首先，我们可以从上面这些数据里面提炼出参加测试的人：
$$P(TESTED)= \frac {TESTED}{N}=0.031768\%$$
然后我们可以找出那些已经参加过测试，然后结果是生病的人数：
$$P(INFECTED|TESTED)= \frac {POSITIVE}{TESTED}=13.7091731\%$$
我们有一个未知数，那就是$P(TESTED|INFECTED)$。那些已经感染了的人，他们会参加测试的概率，我们用一个未知数$π$来表示。
如果我想要知道真实的感染率$P(INFECTED)$，利用贝叶斯的公式，我们可以得出：
$$P(INFECTED|TESTED)=\frac{π×P(INFECTED)}{P(TESTED)}$$
套上已知数,我们得到：
$$13.7091731 \%=\frac{πP(INFECTED)}{0.031768 \%}$$
换一下位置：
$$P(INFECTED)=\frac {13.7091731 \% * 0.031768 \%}{π}$$
现在我们来解决这个π。你可以去CDC公布的数据
具体看这张图：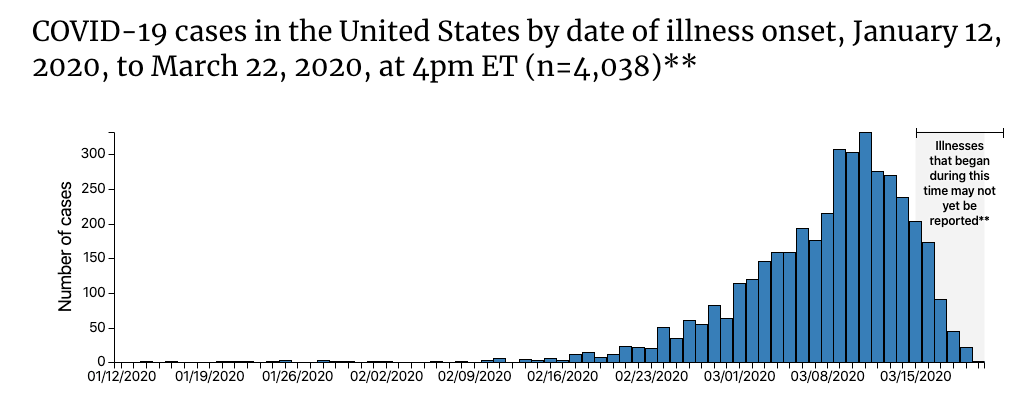
covid-19
这是CDC公布的真实感染人数（测试 + 没测试）。你可能好奇，为什么没测试的人他们也知道。这是他们后面更新的，比如说我3月20日接到一个病人，问他什么时候开始发烧的，他说4天前，那CDC就要往前再加14天（潜伏期），也就是3月12日的时候被感染的，然后3月12日的数据加1。我写这篇博客的时候使用的数据是3月19日的，这部分的数据还没有完全整理出来，一旦整理出来我们就可以知道$π$是啥了。
假设人们都很自觉，80%的人生病了第一时间就会去检测。那么我们可以得到一个:
$$P(INFECTED)=\frac {13.7091731\%×0.031768\%} {0.8}=0.00544391\%$$
那么真实的感染率是0.00544391%，乘以美国人口327200000，大概是17813人被感染。如果你对贝叶斯公式感兴趣可以看看下面几个视频