Introduction
Motivation: we want a data structure to store elements that offers efficient, arbitrary retrieval
(search), insertion, and deletion
- Array-based Lists
- $O(n)$ insertion and deletion
- Fast index-based retrieval
- Efficient binary search if sorted
- Linked Lists
- Efficient, $O(1)$ insert/delete for head/tail
- Inefficient, $O(n)$ arbitrary search/insert/delete
- Efficient binary search not possible without random access
- Stacks and queues are efficient, but are restricted access data structures
- Possible alternative: Trees
- Trees have the potential to provide $O(\log n)$ efficiency for all operations
Definitions & Terminology
- • A
treeis an acyclic graph - For our purposes: a
treeis a collection ofnodes(that can hold keys, data, etc.) that
are connected byedges - Trees are also
oriented: each node has a parent and children - A node with no parents is the
rootof the tree, all child nodes are oriented downward - Nodes not immediately connected can have an ancestor, descendant or cousin relationship
- A node with no children is a
leaf - A tree such that all nodes have at most two children is called a
binary tree - A binary tree is also oriented horizontally: each node may have a left and/or a right
child - Example
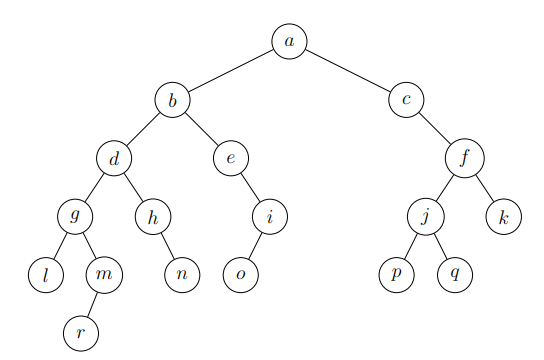
Properties:
In a tree, all nodes are connected by exactly one unique path
The maximum number of nodes at any level $k$ is $2^k$
Thus, the maximum number of nodes n for any binary tree of depth d is:
$$
n=2^0+2^1+2^2+2^{d-1}+2^d = \sum_{k=0}^d 2^k = 2^{d+1}-1
$$Given a full binary tree with n nodes in it has depth:
$$
d=log(n+1)-1
$$That is, $d=O(logn)$
Motivation: if we can create a tree-based data structure with operations proportional to its depth, then we could potentially have a data structure that allows retrieval/search, insertion, and deletion in $O(log n)-time$.