Quick Sort

Pseudocode

Analysis

• Performance of quick sort is highly dependent on how the even the partitioning is
• Partitioning depends on pivot choice

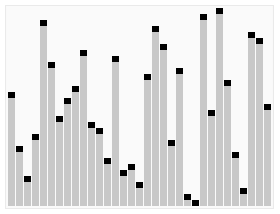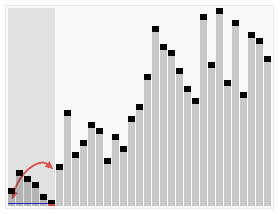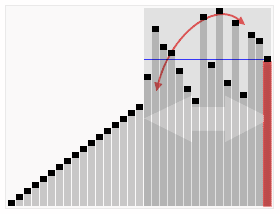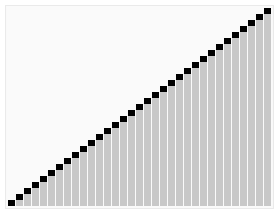
Best Case

• Ideal pivot choice: always choose the median element
• Evenly divides the list into two equal parts
• Two calls to quick sort on lists roughly half the size
• A linear number of comparisons to partition
• Recurrence: $$C(n)=2C(\frac{n}{2})+n$$
• By the Master Theorem, $O(n log n)$

Worst Case

• Worst pivot choice: an extremal element
• Divides into an empty list and a list of size $(n − 1)$
• Only one recursive call is necessary, but on a list of size $(n − 1)$
• Recurrence: $$C(n) = C(n − 1) + n$$
• Back substitution yields $O(n^2)$

Average Case

• Even if the list is is split by a constant proportion, still $O(n log n)$
• A careful average case analysis also yields $$C(n) ≈ 1.38n log n$$
• Still O(n log n)

Pivot Choice: Pivot choice greatly affects performance; several strategies:

• Median-of-Three – Among three elements choose the median.
– Guarantees that the pivot choice will never be the worst case.
– Does not guarantee $Θ(n log n)$.
• Random Element – Randomly select an index for a pivot element.
– Guarantees average running time of $Θ(n log n)$.
– Extra work to randomly select a pivot.
• Linear Time Median Finding.
– An algorithm exists that runs in $Θ(n)$ time to find the median of $n$ objects.
– Guarantees $Θ(n log n)$ in all cases.
– Complicated; recursive; huge overhead.

Code Samples

Code Sample 15: Java Quick Sort for integers

private static void quickSort (int a [] , int left , int right ) {
  int index = partition (a , left , right ) ;
  if ( left < index - 1)
    quickSort (a , left , index - 1) ;
  if ( index < right )
    quickSort (a , index , right ) ;
}

Code Sample 16: Java Partition subroutine for integers

public static int partition (int a [] , int left , int right )
{
  int i = left , j = right ;
  int tmp ;
  int pivot = a [( left + right ) / 2];
  while ( i <= j ) {
    while ( a [ i ] < pivot )
      i ++;
      while ( a [ j ] > pivot )
        j - -;
        if ( i <= j ) {
          tmp = a [ i ];
        a [ i ] = a [ j ];
        a [ j ] = tmp ;
        i ++;
        j - -;
      }
    }
  return i ;
}

Code Sample 17: C Quick Sort for integers

void swap (int *a , int * b )
{
  int t =* a ; * a =* b ; * b = t ;
}
void sort (int arr [] , int beg , int end )
{
  if ( end > beg + 1)
  {
    int piv = arr [ beg ] , l = beg + 1, r = end ;
    while ( l < r )
    {
      if ( arr [ l ] <= piv )
      l ++;
    else
    swap (& arr [ l ] , & arr [ - - r ]) ;
    }
    swap (& arr [ - - l ] , & arr [ beg ]) ;
    sort ( arr , beg , l ) ;
    sort ( arr , r , end ) ;
  }
}

A good tutorial with a non-recursive C implementation: http://alienryderflex.com/quicksort/