COVID-19 and Bayes' Theorem [Written in Chinese]

This post was writteen in Chinese，Original Post.
Since this post had not been translate to English，Please use the tool provided to translate.

Updated Apr 1, 2020. According to the data, not 80% of the people were sick to test the first time, the data far exceeded the estimated 17,813 people. For detailed data, please refer to COVID-19 Tracker - Bing

英国学者托马斯·贝叶斯(Thomas Bayes)提出了一个定理，这个定理的公式如下
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$
其中A,B是两个随机事件，且B事件的发生概率不为零。

P(A)是A事件会发生的概率，P(B)是B事件会发生的概率，P(A|B)是B发生后A会发生的概率，反之亦然。
打个比方:

P(小明迟到) = 0.3 的意思是小明会迟到的概率为30%

P(老板考察出勤) = 0.2 的意思是老板会考察出勤的概率是20%

P(小明迟到 | 老板考察出勤) = 0.25 的意思是老板考察出勤的时候碰巧小明迟到了的概率是25%

通过上面这三个已知条件，我就能通过贝叶斯公式推测出P( 老板考察出勤 | 小明迟到)，即小明今天迟到了，老板刚好要靠勤的概率。
$$P(老板考察出勤|小明迟到) = \frac {0.25×0.3}{0.2}=0.375$$
我想，我可以用这个公式来推导一下新冠肺炎的真实感染人数。下面的计算过程可能会很枯燥，但是结果很有意思。

我们知道美国的人口大概是327,200,000 (三亿两千七百二十万)。截至三月十九，美国一共测试了103,945(十万三千九百四十五)人，其中检查出14,250(一万四千二百五十人)。我们已知的信息有

1
2
3

N = 327200000 # population in the United States
TESTED = 103945 # total test
POSITIVE = 14250 # positive case

首先，我们可以从上面这些数据里面提炼出参加测试的人：
$$P(TESTED)= \frac {TESTED}{N}=0.031768\%$$
然后我们可以找出那些已经参加过测试，然后结果是生病的人数：
$$P(INFECTED|TESTED)= \frac {POSITIVE}{TESTED}=13.7091731\%$$
我们有一个未知数，那就是$P(TESTED|INFECTED)$。那些已经感染了的人，他们会参加测试的概率，我们用一个未知数$π$来表示。
如果我想要知道真实的感染率$P(INFECTED)$，利用贝叶斯的公式，我们可以得出：
$$P(INFECTED|TESTED)=\frac{π×P(INFECTED)}{P(TESTED)}$$
套上已知数,我们得到：
$$13.7091731 \%=\frac{πP(INFECTED)}{0.031768 \%}$$
换一下位置：
$$P(INFECTED)=\frac {13.7091731 \% * 0.031768 \%}{π}$$
现在我们来解决这个π。你可以去CDC公布的数据
具体看这张图：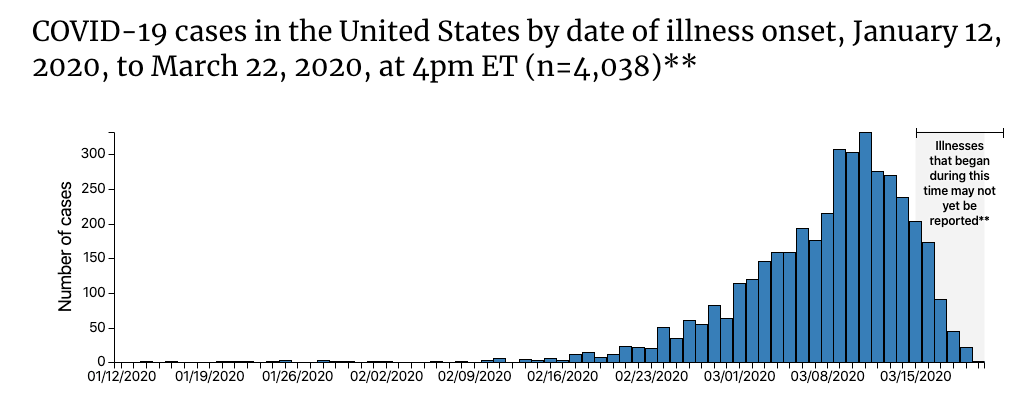
covid-19
这是CDC公布的真实感染人数（测试 + 没测试）。你可能好奇，为什么没测试的人他们也知道。这是他们后面更新的，比如说我3月20日接到一个病人，问他什么时候开始发烧的，他说4天前，那CDC就要往前再加14天（潜伏期），也就是3月12日的时候被感染的，然后3月12日的数据加1。我写这篇博客的时候使用的数据是3月19日的，这部分的数据还没有完全整理出来，一旦整理出来我们就可以知道$π$是啥了。
假设人们都很自觉，80%的人生病了第一时间就会去检测。那么我们可以得到一个:
$$P(INFECTED)=\frac {13.7091731\%×0.031768\%} {0.8}=0.00544391\%$$
那么真实的感染率是0.00544391%，乘以美国人口327200000，大概是17813人被感染。如果你对贝叶斯公式感兴趣可以看看下面几个视频